最大似然框架下,假设观测变量有缺失或不可观测的属性时,要用到变分的方法。隐变量模型往往是无监督或者少监督模型,因为监督信息可以看做是包含在缺失的隐变量中的一部分。
注意:
- 缺失观测和样本一一对应,而参数则是所有样本共享的。
- 似然下界的输入是参数和变分分布,梯度回带到参数和分布上。
- 不可处理(intractable)的分布定义为无法计算,且无法求导。
假设输入$(x, z)\in\mathcal{D}=\mathcal{X}\times\mathcal{Z}$中$\mathcal{Z}$空间是无法观测到的,那么我们的目标就变为了最大化对数边缘似然
$$ \tag{1} \max_{\theta\in\Theta}\log\mathcal{L}(\theta;\mathbf{X})=\sum_{x\in\mathbf{X}}\log p_\theta(x)=\sum_{x\in\mathbf{X}}\log\sum_{z\in\mathcal{Z}}p_{\theta}(x, z), $$其中$\mathbf{X}\subset\mathcal{X}$是观测到的数据集。
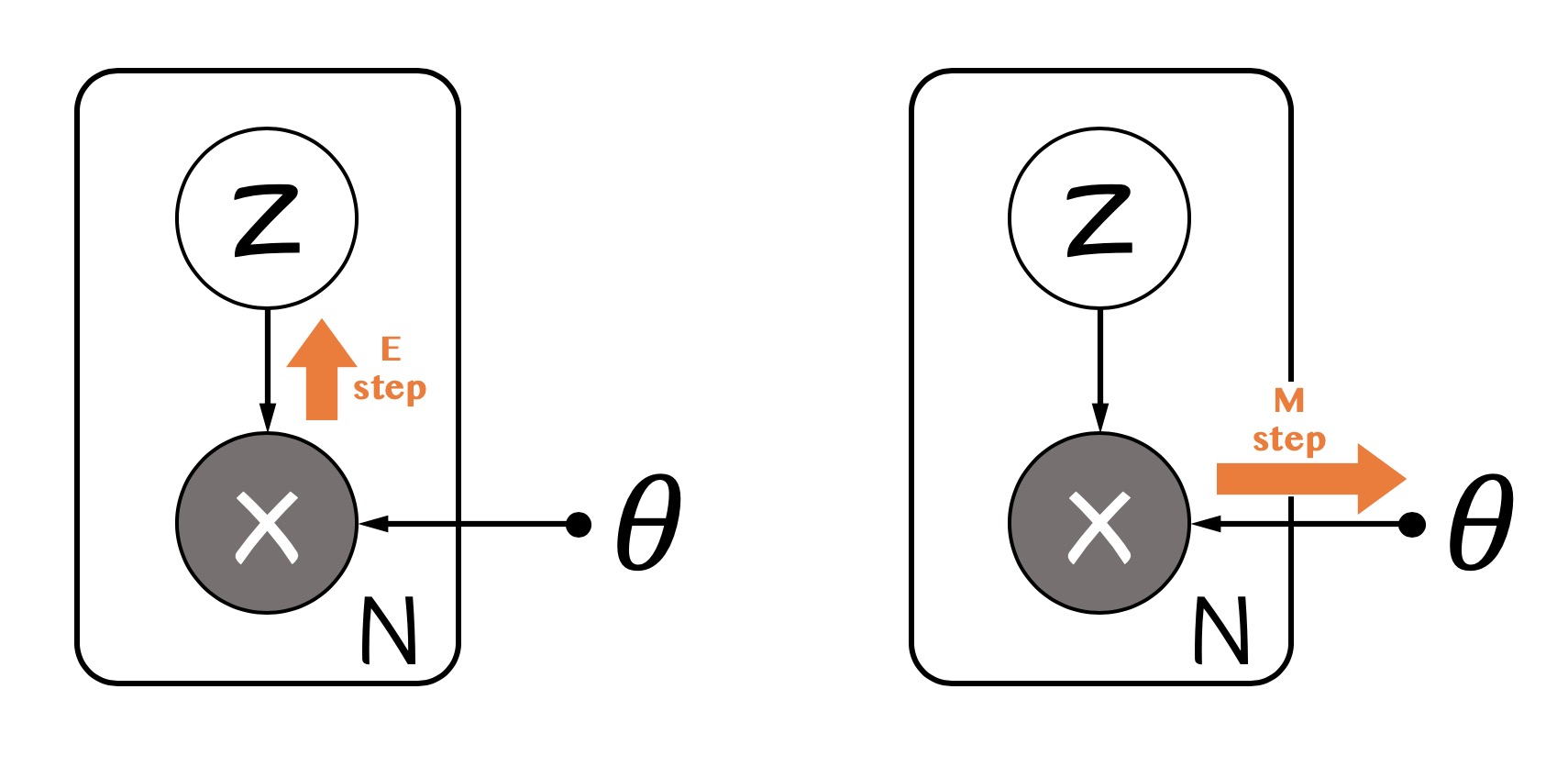
EM算法
直接在式子$(1)$中对$\theta$求导是不好计算的,因为$\log$中有求和。EM算法的思路是优化$(1)$的下界,其核心假设是$p_\theta(x, z)$是很好处理的。利用$\log$函数的凹性和Jensen不等式:
$$ \tag{2} \log\sum_{z\in\mathcal{Z}}p_{\theta}(x, z) = \log\sum_{z\in\mathcal{Z}}\frac{p_{\theta}(x, z)}{q(z)}q(z) \geq \sum_{z\in\mathcal{Z}}q(z)\left\{\log p_\theta(x, z)-\log q(z)\right\}, $$其中$q(z)$是任意定义在$\mathcal{Z}$上的概率密度函数,且$\forall z \in \mathcal{Z} q(z) > 0$。因此之后优化下界
$$ \max_\theta\hat{\mathcal{L}}(q, \theta;\mathbf{X})=\sum_{x\in\mathcal{X}}\sum_{z\in\mathcal{Z}}q(z)\left\{\log p_\theta(x, z)-\log q(z)\right\}. $$这个下界是一个双变量的泛函,一个变量是概率密度$q$,一个变量是参数$\theta$。采用坐标梯度法,交替寻找当前最优的$q$和$\theta$即为EM算法。对$q$取最大要求$(2)$式中等号成立,即要求$\forall z \in \mathcal{Z}, p_\theta(x, z)/q(z)=C$,$C$为某一常数,简单计算一下能得到$C = p_\theta(x)$,而
$$ \tag{E step} q^\star(z)=p_{\theta}(z|x) $$而我们在M步时往往会遇到$\sum_zq(z)\cdot z$这样的$z$的期望形式,因此在实际实现中,我们往往在内存里记录隐变量的期望
$$ \tag{E step in practice} \mathbb{E}[z] = \sum_{z\in\mathcal{Z}}p_\theta(z|x)\cdot z $$这也是E步名字的由来。M步得名原因是我们在这一步里对$\theta$求了最大,注意这个下界往往是凹的(大部分模型是对数凹的,比如GMM中的高斯分布等指数族分布),因此更新的方式为
$$ \tag{M step} \theta^{new} = \arg\max_\theta\sum_{z\in\mathcal{Z}}p_{\theta^{old}}(z|x)\log p_\theta(x, z) $$表示成概率图是这样:
变分EM
变分EM是为了处理全贝叶斯情形下对参数、隐变量的多重积分不可求的问题而发明的。变分(variational)意味着我们要近似一个函数,在一族函数中找一个最能近似目标的。EM算法中的$q(z)$即为一个变分分布,用以近似真实的隐变量后验分布$p_\theta(z|x)$,而变分EM甚至需要对$q(z)$做进一步的近似。
EM算法假设我们有参数$\theta$和隐变量$z$要估计。特别地,对于参数$\theta$我们做的是点估计,是最大似然或者最大后验推断。但是在全贝叶斯方法中,我们对$\theta$也会引入先验分布$p(\theta|\alpha)$,并积分掉$\theta$($\alpha$是超参)。也即现在我们的目标是
$$ \max_\alpha \int p(x|\theta)p(\theta|\alpha) d\theta=\int\int p(x, z|\theta)p(\theta|\alpha)d\theta dz $$我们可以把$\theta$吸收到$z$中,形式上其实和$(2)$一致。即便我们用一个变分分布$q(z, \theta)$来近似$p_\alpha(z, \theta|x)$,在EM算法中往往也会涉及到intractable的积分。一个思路是采样这样的积分,用MCMC方法的思路,这样做的缺点是对每个样本都要做一次采样,对于大数据集计算开销相当大。另一种方法是解耦合这样可以分组的隐变量。
我们假设$q(z, \theta) = q(z)q(\theta)$,或者更一般地,假设$q(z) = \prod_i q_i(z_i)$,即每组隐变量有自己的变分分布且相互独立。假设这样分解以后,对于每个隐变量组$q_i(z_i)$都是tractable的,记$q_i=q_i(z_i)$,单独提取出$z_j$观察下界$\hat{\mathcal{L}}$有
$$ \begin{align} \hat{\mathcal{L}(q)} &= \int \prod_i q_i \left\{\log p(x, z)-\sum_i\log q_i\right\}dz \\ &=\int \prod_i q_i\log p(x, z)dz-\int\prod_iq_i\sum_{i'}\log q_{i'} dz \\ &=\int q_j\left\{\int\log p(x, z)\prod_{i\neq j}q_i dz_i \right\}dz_j - \int \prod_{i} q_i\log q_jdz + \int \prod_i q_i\sum_{i'\neq j}\log q_{i'} dz\\ &= \int q_j \mathbb{E}_{i\neq j}[\log p(x, z)]dz_j - \int q_j\log q_jdz_j + const \end{align} $$把右侧看做一个KL散度,最优的$q_j$满足
$$ \tag{Variational EM} \log q_j^\star(z_j) = \mathbb{E}_{i\neq j}[\log p(x, z)] $$注意到更新$z_j$的分布需要用到$i\neq j$的所有分布来算$p(x, z)$,因此不同的隐变量组的更新是相互依赖的。变分EM迭代地固定$i\neq j$来更新某个隐变量$z_j$,直至所有的隐变量组分布收敛。概率图如下:

VAE
变分自编码器(Variational Auto Encoder)也是隐变量的intractability带来的,不同之处是VAE进一步假设,$p_\theta(x, z), p_{\theta}(z|x)$都是intractable的,且变分将$z$分组也不能使得分布变为tractable的,这样的情形是存在的,比如非线性神经网络。因此我们需要更好的变分方式来近似$p_\theta(z|x)$。VAE提出的方案是用一个由$\phi$控制的分布$q_\phi(z|x)$:
$$ \begin{align} \tag{3} \hat{\mathcal{L}} (\theta, \phi; \mathbf{X}) &= \sum_{x\in\mathcal{X}}\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x, z)-\log q_\phi(z|x)]\\ &= \sum_{x\in\mathcal{X}}\sum_{z\in\mathcal{Z}}q_\phi(z|x)\left\{\log p_\theta(x|z)+\log p_\theta(z)-\log q_\phi(z|x)\right\} \\ \tag{5} & = \sum_{x\in\mathcal{X}}\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)] - \text{KL}\left[q_\phi(z|x)\Vert p_\theta(z)\right] \end{align} $$其中$q_\phi(z|x)$被理解为编码器(Encoder),将观测样本映射到隐变量空间$\mathcal{Z}$,$p_\theta(x|z)$为解码器,将隐变量映射回观测样本空间$\mathcal{X}$。
我们要优化$\hat{\mathcal{L}}$需要对$\theta$和$\phi$求导,其中对$\phi$求导因为期望的存在有几种处理方式。这里看到$\hat{\mathcal{L}}$有$(3)$和$(5)$两种表示,其对$\phi$求导有些问题。
Monte Carlo gradient estimator
一般期望对于分布的参数求导可以使用下面的近似
$$ \begin{align} \nabla_\phi\mathbb{E}_{q_\phi(z)}[f(z)] &= \int f(z) \nabla_\phi q_\phi(z) dz \\ &=\int f(z) q_\phi(z) \frac{\nabla_\phi q_\phi(z)}{q_\phi(z)} dz\\ &=\int f(z)q_\phi(z)\nabla_\phi\log q_\phi(z) dz\\ &=\mathbb{E}_{q_\phi(z)}[f(z)\nabla_\phi\log q_\phi(z)] \\ &\simeq \frac{1}{L}\sum_{l=1}^{L}f(z^{(l)})\nabla_\phi\log q_\phi(z^{(l)}) \end{align} $$但是这样得到的近似方差很大,需要较大的$L$来保证一个很好的梯度估计(详见这篇文章)。在$(3)$中我们可以用类似的方式得到$\hat{\mathcal{L}}$对$\phi$的导数,但是较大的$L$使得每个样本的采样代价高,因此在大数据集上没有办法应用。
Reparameterization trick (SGVB estimator)
对于式$(3)$中的期望,如果我们对$z$节点进行采样近似以后,再算对$\phi$的导数会得到不正确的结果,因为采样的分布$q_\phi(z|x)$是依赖$\phi$的,概率图如下:
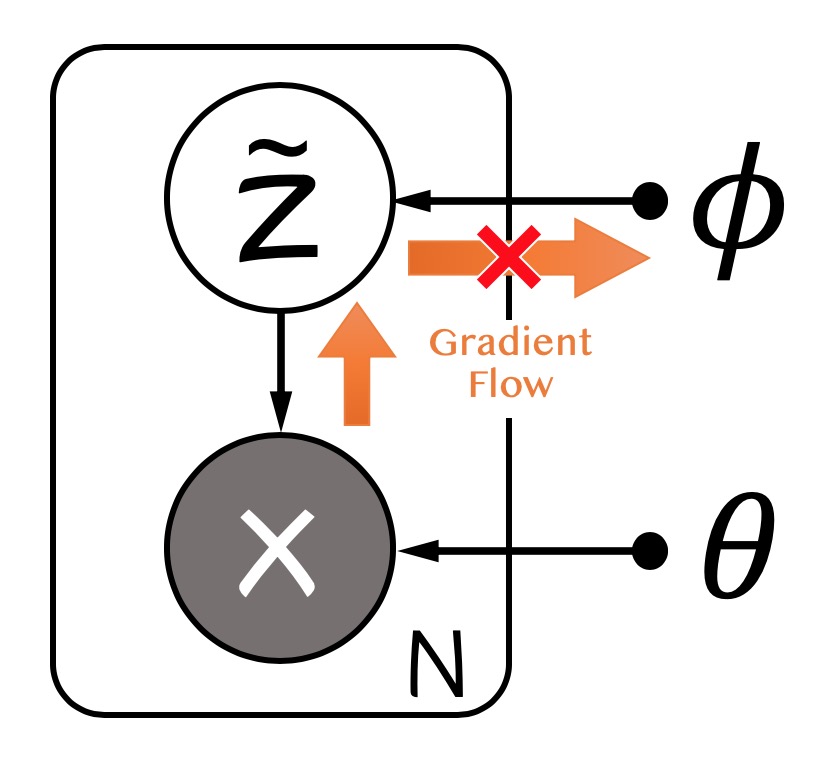
Reparameterization将随机性的来源从$z$转移到另一个辅助的噪声变量$\epsilon$,假设$z=g_\phi(\epsilon, x)$,其中$\epsilon\sim p(\epsilon)$,$(3)$式变为
$$ \begin{align} \hat{\mathcal{L}}{}^A(\phi, \theta;\mathbf{X}) &= \sum_{x\in\mathcal{X}}\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x, z)-\log q_\phi(z|x)] \\ &=\sum_{x\in\mathcal{X}}\mathbb{E}_{p(\epsilon)}[\log p_\theta(x, g_\phi(\epsilon, x))-\log q_\phi(g_\phi(\epsilon, x)|x)]\\ &\simeq \sum_{x\in\mathcal{X}}\frac{1}{L}\log p_\theta(x, g_\phi(\epsilon^{(l)}, x))-\log q_\phi(g_\phi(\epsilon^{(l)}, x)|x) \end{align} $$这样的近似比MC梯度近似有更小的方差,且我们可以直接对损失函数进行近似。SGVB的概率图如下:

Second Version SGVB estimator
$(3)$式可以化简为$(5)$式,若$(5)$式中的KL散度项可以积分(tractable),我们就可以只对$(5)$式中的第一项进行采样近似,相比于最原始的SGVB估计子,因为只对变分下界$\hat{\mathcal{L}}$的一部分近似,方差会更小:
$$ \hat{\mathcal{L}}{}^B(\phi, \theta; \mathbf{X}) = -\text{KL}\left[q_\phi(z|x)\Vert p_\theta(z)\right] + \frac{1}{L}\sum_{l=1}^L\log p_\theta\left(x\middle|g_\phi(\epsilon^{(l)}, x)\right) $$最后,整个VAE的过程如下:

